Equations différentielles ordre2
Plan du chapitre
Dans le cours et les exemples, est une fonction de la variable . Dans les exercices, la variable peut être soit , soit .
Pour des raisons pratiques, les constantes notées
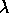 et
et
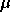 dans le formulaire de BTS sont ici nommées
et
.
dans le formulaire de BTS sont ici nommées
et
.
Dans les réponses aux exercices utilisant ces constantes, il faut écrire le signe * de multiplication, ou laisser un espace.
Pour donner la réponse
, on écrira : k*e^(3t) ou k e^(3t), ou encore k exp(3t), mais pas ke^(3t).
-
Préliminaire : équation du second degré dans
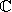
- Equations différentielles de la forme ay'' + by' + cy = 0
- Equation caractéristique
- 1° cas : l'équation caractéristique a deux solutions réelles
- 2° cas : l'équation caractéristique a une solution réelle
- 3° cas : l'équation caractéristique a deux solutions complexes non réelles
- Conditions initiales
- Equations différentielles de la forme ay'' + by' + cy = φ(t)
Solutions complexes des équations du second degré à coefficients réels
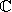 est l'ensemble des nombres de la forme
où
est l'ensemble des nombres de la forme
où
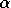 et
et
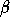 sont deux réels et
est un nombre (non réel) qui vérifie
sont deux réels et
est un nombre (non réel) qui vérifie
On s'intéresse ici uniquement aux équations de la forme
où
,
et
sont réels (avec
) et où l'inconnue
appartient à
Méthode
- Calculer le discriminant : .
- Regarder le signe de
 .
.
Il est strictement positif, donc l'équation a deux solutions réelles.
Ces solutions sont : et
Il est nul, donc l'équation a une solution réelle.
Cette solution est :
Exercice
Equations différentielles de la forme ay'' + by' + cy = 0
désigne une fonction de la variable ,
désigne la dérivée de ,
et désigne la dérivée seconde de , c'est à dire la dérivée de
les coefficients , et sont des constantes réelles.
Pour résoudre une équation de ce type, on commence par écrire son équation caractéristique .
Equation caractéristique associée à une équation différentielle
On résout cette équation dans
 .
.
On a donc trois cas selon que est strictement positif , nul , ou strictement négatif .
Cas 1 : Δ > 0
Si l'équation caractéristique a deux solutions réelles et , alors l'équation différentielle admet comme solutions les fonctions :
Son discriminant est : .
L'équation caractéristique a deux solutions réelles : et
Les solutions de sont donc les fonctions , où et sont deux constantes réelles.
Exercice
Cas 2 : Δ = 0
Il y a donc une (double) infinité de solutions à cette équation.
Son discriminant est : .
L'équation caractéristique a une solution réelle : .
Les solutions de sont donc les fonctions , où et sont deux constantes réelles.
Exercice guidé sur le cas 2
Exercice sur le cas 2
Exercice sur le cas 1 ou le cas 2
Cas 3 : Δ < 0
Il y a donc une (double) infinité de solutions à cette équation.
Son discriminant est : .
L'équation caractéristique a deux solutions complexes non réelles : et
Les solutions de sont donc les fonctions , où et sont deux constantes réelles.
Exercice sur le cas 3
Exercice sur l'ensemble de tous les cas
Conditions initiales
Pour traduire ces conditions, on doit donc commencer par dériver la formule trouvée pour la solution générale (sans oublier que h et k sont deux constantes).
En écrivant ces conditions, on obtient un système de deux équations à deux inconnues h et k, qui se résout à l'aide des méthodes "habituelles". Quand t0 = 0, le système obtenu est en général simple à résoudre.
Remarque : D'autres types de conditions initiales peuvent également, selon les cas, donner une solution unique les vérifiant. Il faut en général deux conditions pour trouver les deux constantes.
Discriminant : .
Solution(s) de l'équation caractéristique : -5 et
La dérivée de
est
f'(t) =.
On a donc (en remplaçant
t par 0) :
et
Le système
devient :
Ce système a comme solution :
Donc
f(t) =.
Exercice avec des équations de type 1 et 2
Equations différentielles de la forme ay'' + by' + cy = φ(t)
Pour résoudre (E), on a besoin de résoudre (E0). Il faut donc déjà savoir faire les exercices de la partie précédente.
Théorème fondamental
La solution générale de l'équation (E) est la somme d'une solution particulière de (E) et de la solution générale de (E0)
La méthode pour trouver la solution générale de (E0) a été étudiée dans les pages précédentes du cours.
Les méthodes pour trouver une solution particulière de (E) sont dans les pages suivantes.
Recherche d'une solution particulière
Vérifier qu'une fonction donnée est une solution particulière
On commence par calculer la dérivée de
:
(et on la simplifie, si possible).
On calcule la dérivée de
:
(et on la simplifie, si possible).
On calcule ensuite
, on le simplifie au maximum et ... on retrouve comme par miracle
.
On en déduit alors que g est une solution particulière de
La dérivée de g'(t) = est g''(t) =.
On a donc : = =
On retrouve bien le second membre de l'équation différentielle
.
Ceci prouve que la fonction
g est une solution particulière de
.
Déterminer une solution particulière de forme donnée
On commence par calculer la dérivée de
:
(et on la simplifie, si possible).
On calcule la dérivée de
:
(et on la simplifie, si possible).
On calcule ensuite
, on le simplifie au maximum en regroupant les termes pour ressembler au maximum à
.
On identifie alors les coefficients entre le résultat trouvé et . On obtient ainsi un système permettant de trouver les paramètres cherchés. On les remplace enfin dans l'expression de g(t) pour conclure.
La dérivée de g'(t) = est g''(t) = =.
On a donc : = =
On identifie avec le second membre de l'équation différentielle
.
En résolvant le système obtenu, on trouve
.
La fonction
est donc une solution particulière de
.
Exercice avec calculs de dérivées pas trop compliqués
Exercice
Résolution de l'équation ay'' + by' + cy = φ(t)
- écrire l'équation homogène (E0) associée :
- résoudre (E0): on appelle "solution générale" de (E0) l'ensemble de toutes les solutions de (E0) (dépendant de deux constantes)
- déterminer une solution particulière de (E)
- la solution générale de (E) est la somme de la solution particulière (étape 3) et de la solution générale de (E0) (étape 2)
Résolution de l'équation homogène associée
L'équation homogène associée à est : .Le discriminant de l'équation caractéristique est : .
L'équation caractéristique a donc deux solutions : r1 = 5 et r2 =.
Les solutions de sont donc les fonctions , où et sont deux constantes réelles.
Recherche d'une solution particulière
La dérivée de est g'(t) = =.La dérivée de g'(t) = est g''(t) = =.
On a donc : = =
On identifie avec le second membre de l'équation différentielle
.
En résolvant le système obtenu, on trouve
.
La fonction
est donc une solution particulière de
.
Solution générale
On ajoute la solution générale de l'équation homogène (E0), c'est à dire et une solution particulière de (E), c'est à dire .La solution générale de (E) est donc .
Résolution avec conditions initiales
Pour traduire ces conditions, on doit donc commencer par dériver la formule trouvée pour la solution générale (sans oublier que h et k sont deux constantes).
En écrivant ces conditions, on obtient un système de deux équations à deux inconnues h et k, qui se résout à l'aide des méthodes "habituelles". Quand t0 = 0, le système obtenu est en général simple à résoudre.
Déterminer la solution de cette équation qui vérifie : et .
Equation homogène associée
Son équation caractéristique est : .
Le discriminant de l'équation caractéristique est : .
L'équation caractéristique a donc deux solutions : r1 = -4 et r2 =.
Les solutions de sont donc les fonctions , où et sont deux constantes réelles.
Solution particulière de (E)
g'(t) =
g''(t) =
On a donc : =
On identifie avec le second membre de l'équation différentielle et on résout le système obtenu, d'où : .
La fonction est donc une solution particulière de .
Solution générale de (E)
La solution générale de
(E) est donc .
Solution de
(E) qui vérifie les conditions initiales
La fonction
f doit être une solution de
(E), donc
.
Une des conditions initiales concerne
, donc on calcule
f'(t) =.
En remplaçant
t par 0, on trouve :
et
.
Les conditions initiales
deviennent donc :
C'est un système de deux équations à deux inconnues
h et
k qui a comme solution :
Exercice (avec calcul de dérivées pas trop compliqué)
Exercice
Remarque : D'autres types de conditions initiales peuvent également, selon les cas, donner une solution unique les vérifiant. Il faut en général deux conditions pour trouver les deux constantes.